Найти тангенс арккотангенса, пользуясь определениями тангенса и котангенса в прямоугольном треугольнике и определением арккотангенса, можно легко, и дополнительные тригонометрические формулы для этого не нужны.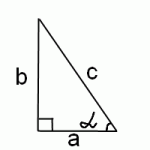
Чтобы найти tg (arcctg x), вспоминаем, что арккотангенс икса — это такое число альфа, котангенс которого равен икс:
![\[arcctgx = \alpha , \Rightarrow ctg\alpha = x.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-aa31b37e1cc2d2cbb3a450c31fadadf6_l3.png "Rendered by QuickLaTeX.com")
А поскольку котангенс в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему, то в нашем случае
![\[ctg\alpha = \frac{a}{b}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-fe485535ea452164b0ef760df792b2c0_l3.png "Rendered by QuickLaTeX.com")
Нам нужен тангенс этого же угла, а он равен отношению противолежащего катета к прилежащему, то есть b к a. Отсюда
![\[tg(arcctg\frac{a}{b}) = \frac{b}{a}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ad31f11949e6d12075969d052f11170f_l3.png "Rendered by QuickLaTeX.com")
Если нужно найти арккотангенс отрицательного числа, то есть tg (arcctg (-x)), то используя свойство арктангенса arcctg (-x)=π-arcctg x и формулу приведения
tg(π-α)=-tg α, получаем, что
tg (arcctg (-x))=tg (π-arcctg x)=-tg(arcctg x).
Пример.
Найти tg (arcctg (-2/3)).
Решение: tg (arcctg (-2/3))=tg (π-arcctg(2/3))= — tg (arcctg (2/3)).
Рассуждая аналогично изложенному выше, приходим к выводу: tg (arcctg (2/3))=3/2, следовательно,
tg (arcctg (-2/3))=- 3/2.