Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.
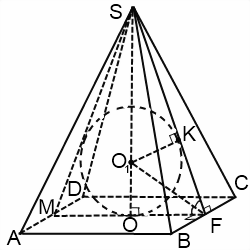
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.
В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.
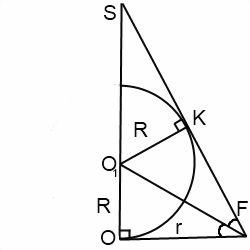 Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Итак, в прямоугольном треугольнике SOF катет SO=H — высота пирамиды, катет OF=r — радиус вписанной в основание пирамиды окружности, гипотенуза SF=l — апофема пирамиды. O1- центр шара и, соответственно, окружности, вписанной в треугольник, полученный в сечении (мы рассматриваем его часть). Угол SFO — линейный угол двугранного угла между плоскостью основания и плоскостью боковой грани SBC. Точки K и O — точки касания, следовательно, O1K перпендикулярен SF. OO1=O1K=R — радиусу шара.
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.
Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что
![]()
В треугольнике SOF применим свойство биссектрисы треугольника:
![]()
Из прямоугольного треугольника OO1F
![]()
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.
![]()
![]()
![]()
Теперь найдем отношение объема пирамиды к площади ее поверхности:
![]()
![]()
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:
![]()
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).
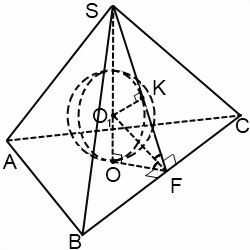
«Катет OF=r — радиус вписанной в основание пирамиды окружности», разве r — радиус вписанной окружности в основание? По-моему это радиус описанной около основания окружности.
OF — перпендикуляр, проведенный из центра правильного многоугольника к его стороне. Описанная же окружность проходит через вершины многоугольника.
А что, если пирамида неправильная?? Этот случай не разобран, а интересно.
Алексей, когда-нибудь разберу и этот случай, но сроков не называю — не хватает времени, увы.
Верна ли формула для нахождения радиуса вписанного шара в тетраэдр для случая, когда шар вписан в неправильный тетраэдр?
Спасибо
Для пирамиды, у которой двугранные углы при основании равны — да, в общем случае — нет.
>>Точки K и O — точки касания, следовательно, O1K перпендикулярен SF.
Где точное обоснование данного вывода?
Ириэ, это следует из свойства касательной: касательная перпендикулярна радиусу, проведённому в точку касания.
Очень хороший разбор, но в конце мне кое что непонятно, вы не могли бы объяснить?
Сори, разобралась) по-видимому, этот вывод формулы действует только в том случае, если в основании пирамиды лежит квадрат. Я верно поняла??
Да, верно. Поскольку речь здесь идёт о правильной пирамиде. Основание правильной четырёхугольной пирамиды — квадрат.
Большое спасибо, реально очень помогло!