« »

Рубрика: Легкое решение

Найти тангенс арккосинуса

Легко найти тангенс арккосинуса tg (arccos x) с помощью определений тангенса, косинуса, арккосинуса и теоремы Пифагора. При таком решении не нужно привлекать какие-либо тригонометрические формулы.

По определению арккосинуса:

    \[\arccos x = \alpha , \Rightarrow x = \cos \alpha .\]

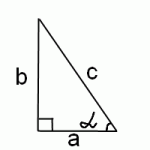
Но косинус угла альфа  в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:

    \[\cos \alpha = \frac{a}{c}.\]

Нам нужен тангенс этого же угла альфа. А тангенс — это отношение противолежащего катета к прилежащему:

    \[tg\alpha = \frac{b}{a},\]

а значит, задача сводится к нахождению противолежащего катета b. По теореме Пифагора:

    \[b = \sqrt {{c^2} - {a^2}} ,\]

откуда искомое значение тангенса арккосинуса tg (arccos x) —

    \[tg(\arccos x) = \frac{{\sqrt {{c^2} - {a^2}} }}{a},\]

где

    \[x = \frac{a}{c}.\]

Все. Никаких дополнительных формул применять не нужно.

Примеры.

1) Найти tg (arccos 1/3).

arccos 1/3- это такое число альфа, что cos α =1/3. В прямоугольном треугольнике косинус равен отношению прилежащего катета к гипотенузе, значит, в нашем случае прилежащий катет a=1, гипотенуза с=3. Нам нужно найти тангенс этого же угла α, а тангенс равен отношению противолежащего катета к прилежащему. Осталось по теореме Пифагора найти противолежащий катет:

    \[b = \sqrt {{3^2} - {1^2}} = \sqrt 8 = 2\sqrt {2.} \]

Таким образом, искомое значение tg (arccos 1/3)

    \[tg(\arccos \frac{1}{3}) = \frac{{2\sqrt 2 }}{1} = 2\sqrt 2 .\]

2) Найти tg (arccos 3/5).

Здесь прилежащий катет a=3, гипотенуза c=5, откуда противолежащий катет

    \[b = \sqrt {{5^2} - {3^2}} = 4, \Rightarrow tg(\arccos \frac{3}{5}) = \frac{4}{3}.\]

2 комментария , 14 Авг 2012

2 комментария на «Найти тангенс арккосинуса»

  1. Лидия:
    28.07.2016 в 10:25 дп

    Очень просто и доступно. Так легко. Спасибо огромное.

    Ответить
  2. Владимир:
    03.04.2017 в 8:54 пп

    Спасибо огромное!! очень помогло))

    Ответить

Ваш отзыв