« »

Рубрика: Задачи на трапецию

В прямоугольную трапецию вписана окружность

Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.

окружность в прямоугольной трапеции

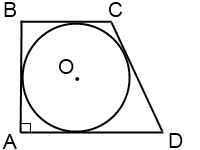
1. Сумма оснований трапеции равна сумме боковых сторон.

2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.

3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.

4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.

5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен

    \[r = \sqrt {mn} \]

(Подробнее смотрите «В трапецию вписана окружность«)

И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:

1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).

2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.

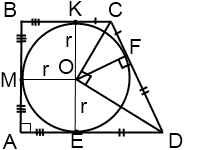в прямоугольную трапецию вписана окружность  Площадь трапеции равна произведению полусуммы ее оснований на высоту:

    \[S = \frac{{AD + BC}}{2} \cdot AB\]

Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

    \[r = \sqrt {mn} , \Rightarrow {r^2} = mn,\]

 

    \[AD = AE + ED = r + n,\]

    \[BC = BK + KC = r + m,\]

    \[S = \frac{{r + n + r + m}}{2} \cdot 2r = (2r + m + n)r = \]

    \[ = 2{r^2} + rm + rn = {r^2} + {r^2} + rm + rn = \]

    \[ = {r^2} + mn + rm + rn = (mn + rm) + ({r^2} + nr) = \]

    \[ = m(n + r) + r(n + r) = (n + r)(m + r) = BC \cdot AD.\]

 

 

10 комментариев , 01 Май 2013

10 комментариев на «В прямоугольную трапецию вписана окружность»

  1. Юрий:
    24.09.2013 в 4:23 пп

    Очень полезная статья, спасибо!

    Ответить
  2. асманти:
    15.04.2014 в 7:14 пп

    спасибо,помогли очень!!!

    Ответить
  3. Татьяна:
    11.03.2015 в 9:26 пп

    Спасибо, выручили!

    Ответить
  4. Рома:
    25.05.2015 в 7:53 пп

    Полезно, спасибо!

    Ответить
  5. Катерина:
    15.06.2015 в 9:51 дп

    Спасибо) жаль только, что узнала об этом интересном свойстве только после экзаменов.

    Ответить
  6. Анна:
    08.01.2017 в 3:49 пп

    Большое спасибо очень нужные свойства

    Ответить
  7. Эдуард:
    20.11.2017 в 9:08 пп

    А может ли радиус равняться h=2r?

    Ответить
    • Светлана Иванова:
      09.12.2017 в 12:42 пп

      Эдуард, высота h равна двум радиусам. Именно это подразумевает формула h=2r.

      Ответить
  8. Николай:
    02.11.2021 в 9:40 пп

    Привет из 2021!
    Огромное спасибо за статью: очень полезная и удобная (все правила на одну тему сразу написаны).

    Ответить

Ваш отзыв