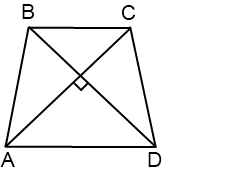
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
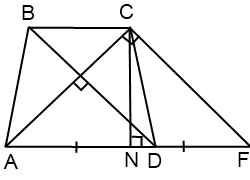
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
![\[CN = \frac{1}{2}AF = \frac{{AD + BC}}{2},\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ea1bd5a263ee8f32ef460ec860366791_l3.png "Rendered by QuickLaTeX.com")
что в общем виде можно записать как
![\[h = \frac{{a + b}}{2},\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-f4ba83d9b9f1a3bee519b150fce31e48_l3.png "Rendered by QuickLaTeX.com")
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
![\[h = m.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-118549c3f48ca44b9cc35cbc362f363e_l3.png "Rendered by QuickLaTeX.com")
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
![\[S = \frac{{a + b}}{2} \cdot h\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-da31aa3f55040eba461d39cf01cae001_l3.png "Rendered by QuickLaTeX.com")
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
![\[h = \frac{{a + b}}{2} = m,\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-9f388ae263dd9f799f988c8b1a65afac_l3.png "Rendered by QuickLaTeX.com")
то
![\[S = {h^2}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d54b697b47d33294fe1697e987a23635_l3.png "Rendered by QuickLaTeX.com")
![\[S = {(\frac{{a + b}}{2})^2}\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-a4c18a134c1022b435cde9ac2b1488b0_l3.png "Rendered by QuickLaTeX.com")
![\[S = {m^2}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-1e8ce2a2f2543d3c352f74c117498efa_l3.png "Rendered by QuickLaTeX.com")
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
![\[S = \frac{1}{2}{d_1}{d_2}\sin \varphi \]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-41abaa83a54aed4793cbbb3129378fc9_l3.png "Rendered by QuickLaTeX.com")
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
![\[S = \frac{1}{2}{d^2}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-c6001b807afd5954f49c304fbec201a0_l3.png "Rendered by QuickLaTeX.com")
откуда
![\[\frac{1}{2}{d^2} = {(\frac{{a + b}}{2})^2} = {h^2} = {m^2},\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-8edee54e09bcfdabc6c4568eac7fdf26_l3.png "Rendered by QuickLaTeX.com")
![\[{d^2} = \frac{{{{(a + b)}^2}}}{2}.\]](https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-c40f7932b4862ad077bea46e66283904_l3.png "Rendered by QuickLaTeX.com")
очень позновательно и интересно! прекрасная статья очень помогла при решении!! спасибо очень благодарна
Алина, спасибо за теплый отзыв! Я рада, что информация Вам пригодилась. Успехов Вам в учебе!
а чё этого нет у нас в книге а то полдня решал и так доказал эту 3 теорему
Чтобы ученики научились часть материала находить или доказывать самостоятельно 🙂
И зачем все так усложнять? На какой нам дополнительное построение? Можно доказать, что высота равна полусумме оснований через равнобедренные треугольники, проведя две высоты. К примеру ОН в треугольнике ВОС и ОК в треугольнике АОД. Так, как треугольники прямоугольные и равнобедренные углы по 45 градусов, а значит медианы (они же высоты) будут равняться половинам основаниям, каждая соответственно. А в сумме они и будут давать высоту равную а+b/2….
Тем и хороша геометрия, что решение одной и той же задачи можно вести разными путями.
Спасибо за интересную подборку задач!
спасибо выручили
действительно, очень полезный сайт! Спасибо Вам огромное! никогда не думал, что из перпендикулярных диагоналей следует столько выводов и формул:)
Спасибо большое, очень полезная статья, полдня мучилась с задачей, думала, какую-то формулу не выучила или что-то ещё. В общем, спасибо! 🙂
Огромное спасибо :3
Спасибо огромное ,очень помогло!!
Большое спасибо, объяснила внуку и сама получила информацию
Такие штучки в шк не говорят, а ряд задач решить без них оч сложно.
Спасибо!
П.С. Где бы найти все useful формулы по геом? Для физ-мата
Почему в школе нет такого материала о равнобедренной трапеции, по сути это ключевая задача, а метод доказательства просто универсален, задача очень помогла. Спасибо
Помогите решить задачу в равнобедренной трапеции диагонали которой перпендикулярны меньшее основание 12 см, а большее 16. Найдите высоту и площадь трапеции
Boris, всё, что Вам надо для решения задачи, расписано выше.
Спасибо!!! Так выручили!!!!
Пожалуйста!
А что это за теорема ?
Скорее, опорная задача. Впрочем, можете назвать её и теоремой.
Спасибо! Очень помогает в решении некоторых, с виду очень простых, задач!