« »

Рубрика: Задачи на трапецию

В равнобедренную трапецию вписана окружность

Рассмотрим частный случай вписанной в трапецию окружности.

Если в равнобедренную трапецию вписана окружность, существует несколько направлений, по которым можно повести решение задачи.

1. В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n. Найти площадь трапеции.

Решение:

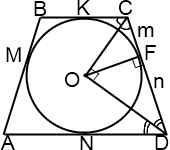 в равнобедренную трапецию вписана окружность1)∠ADC+∠BCD=180º(как внутренние односторонние при AD∥BC и секущей CD).

2) Так как центр вписанной окружности — точка пересечения биссектрис трапеции, то

∠OCD+∠ODC=90º.

3) Так как сумма углов треугольника равна 180º, в треугольнике OCD ∠COD=90º.

4) OF перпендикулярен CD (как радиус, проведенный в точку касания), следовательно, в треугольнике OCD OF — высота, проведенная к гипотенузе. По свойству прямоугольного треугольника,

    \[OF = \sqrt {CF \cdot FD} \Rightarrow r = \sqrt {mn} \]

Так как высота трапеции равна диаметру вписанной окружности, то

    \[h = 2r = 2\sqrt {mn} .\]

5) Формула для нахождения площади трапеции

    \[S = \frac{{a + b}}{2} \cdot h\]

Так как в трапецию вписана окружность, суммы ее противолежащих сторон равны:

    \[AD + BC = AB + CD = 2CD = 2(m + n).\]

Таким образом, площадь трапеции равна

    \[S = \frac{{2(m + n)}}{2} \cdot 2\sqrt {mn} = 2(m + n)\sqrt {mn} .\]

2. В равнобедренную трапецию вписана окружность, которая в точке касания делит боковую сторону на отрезки m и n.Найти периметр трапеции.

Решение:

 

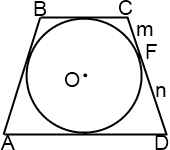точка касания окружности делит боковую сторону  CD=CF+FD=m+n.

AB=CD (по условию).

AD+BC=AB+CD (так как в трапецию вписана окружность).

P=AD+BC+AB+CD=4(m+n).

 

3.В равнобедренную трапецию вписана окружность. Найти высоту трапеции, если известны ее основания: AD=a, BC=b.

Решение:

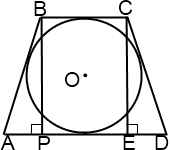Найти высоту трапеции  Проведем высоты трапеции BP и CE. Четырехугольник BCEP- прямоугольник (так как у него все углы прямые). Следовательно, PE=BC=b.

Прямоугольные треугольники треугольники ABP и DCE равны по катету и гипотенузе. Отсюда,

    \[AP = DE = \frac{{AD - BC}}{2} = \frac{{a - b}}{2}.\]

Поскольку в трапецию вписана окружность, AB+CD=AD+BC=a+b,

    \[AB = \frac{{AB + CD}}{2} = \frac{{a + b}}{2}.\]

Из треугольника ABPпо теореме Пифагора

    \[B{P^2} = A{B^2} - A{P^2}\]

    \[B{P^2} = {(\frac{{a + b}}{2})^2} - {(\frac{{a - b}}{2})^2} = \]

    \[\begin{array}{l} = (\frac{{a + b}}{2} - \frac{{a - b}}{2})(\frac{{a + b}}{2} + \frac{{a - b}}{2}) = ab.\\A{B^2} - A{P^2}\end{array}\]

Таким образом,

    \[h = \sqrt {ab} \]

Вывод:

Если в равнобедренную трапецию вписана окружность, высота трапеции есть среднее пропорциональное между ее основаниями.

 

 

Ваш отзыв , 17 Июн 2013

Ваш отзыв