« »

Рубрика: Задачи по алгебре

Задачи на концентрацию

Рассмотрим задачи на концентрацию, в которых речь идет о процентном содержании вещества в сплаве или растворе. В этом случае

как найти концентрацию

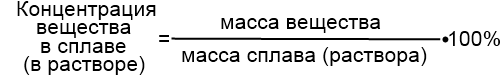
В 8-9 классах задачи на концентрацию решаются чаще всего с помощью дробных рациональных уравнений. В качестве примера рассмотрим две задачи на концентрацию.

1) Водно-солевой раствор содержал 8 граммов соли. Спустя некоторое время 20 граммов воды испарилось, и концентрация соли в растворе увеличилась на 2%. Сколько граммов воды содержал первоначальный  раствор?

Решение:

Пусть х граммов воды содержал первоначальный раствор.

задача на концентрацию

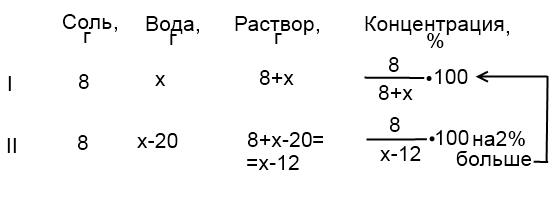
Составим и решим уравнение:

    \[\frac{8}{{x - 12}} \cdot 100 - \frac{8}{{8 + x}} \cdot 100 = 2\]

Обе части уравнения разделим на 2:

    \[\frac{{400}}{{x - 12}} - \frac{{400}}{{8 + x}} = 1\]

Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:

    \[\frac{{{{400}^{\backslash (8 + x)}}}}{{x - 12}} - \frac{{{{400}^{\backslash (x - 12)}}}}{{8 + x}} - {1^{\backslash (8 + x)(x - 12)}} = 0\]

    \[\frac{{400(8 + x) - 400(x - 12) - (8 + x)(x - 12)}}{{(x - 12)(8 + x)}} = 0\]

    \[\frac{{3200 + 400x - 400x + 4800 - 8x + 96 - {x^2} + 12x}}{{(x - 12)(8 + x)}} = 0\]

    \[ \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 4x + 8096 = 0;\\(x - 12)(8 + x) \ne 0.\end{array} \right.\]

    \[x \ne 12;x \ne - 8\]

    \[{x^2} - 4x - 8096 = 0\]

    \[{x_1} = 92;{x_2} = - 88\]

Второй корень не подходит по смыслу задачи, так как масса не может быть отрицательным числом. Значит, первоначальный раствор содержал 92 грамма воды.

Ответ: 92 г.

2) Кусок меди и цинка, содержащий 9 килограммов цинка, сплавили с 3 килограммами меди. В новом сплаве содержание меди на 10% больше, чем в первоначальном. Сколько килограммов меди было в первоначальном сплаве?

Решение:

Пусть х килограммов меди было в первоначальном сплаве.

решение задачи на концентрацию

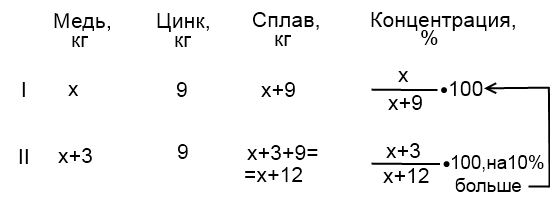
Составим и решим уравнение:

    \[\frac{{x + 3}}{{x + 12}} \cdot 100 - \frac{x}{{x + 9}} \cdot 100 = 10\]

Обе части уравнения делим на 10:

    \[\frac{{10(x + 3)}}{{x + 12}} - \frac{{10x}}{{x + 9}} = 1\]

Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:

    \[\frac{{10{{(x + 3)}^{\backslash (x + 9)}}}}{{x + 12}} - \frac{{10{x^{\backslash (x + 12)}}}}{{x + 9}} - {1^{\backslash (x + 9)(x + 12)}} = 0\]

    \[\frac{{10(x + 3)(x + 9) - 10x(x + 12) - (x + 9)(x + 12)}}{{(x + 9)(x + 12)}} = 0\]

    \[\frac{{10({x^2} + 3x + 9x + 27 - {x^2} - 12x) - ({x^2} + 9x + 12x + 108)}}{{(x + 9)(x + 12)}} = 0\]

    \[\frac{{270 - {x^2} - 21x - 108}}{{(x + 9)(x + 12)}} = 0\]

    \[ \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 21x + 162 = 0;\\(x + 9)(x + 12) \ne 0.\end{array} \right.\]

    \[x \ne - 9;x \ne - 12.\]

    \[{x^2} + 21x - 162 = 0\]

    \[{x_1} = 6;{x_2} = - 27\]

Второй корень не подходит по смыслу задачи, так как масса не может быть отрицательным числом. Значит, в первоначальном сплаве было 6 кг меди.

Ответ: 6 кг.

Задачи на концентрацию, как и задачи на смеси и сплавы, — задачи из курса химии.

5 комментариев , 30 Июн 2013

5 комментариев на «Задачи на концентрацию»

  1. Владимир Владленович:
    12.12.2014 в 11:35 дп

    как сложно!
    проще через формулу сухого вещества

    Ответить
  2. Каришка:
    25.04.2015 в 8:35 пп

    Решение, действительно, сложное
    Предлагаю включить «правило креста». Ответ находится за 3 действия 🙂

    Ответить

Ваш отзыв