Узнать ещё

Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.

I. Биссектрисы углов при боковой стороне трапеции пересекаются.

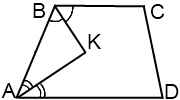 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).

2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).

3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.

Вывод:

Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.

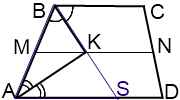 Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.

Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.

Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.

Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

Вывод:

Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.

II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.

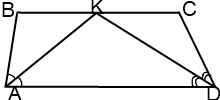 В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.

 

 

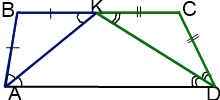 Таким образом, BC=BK+KC=AB+CD.

 

 

 

Вывод:

Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.

В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.

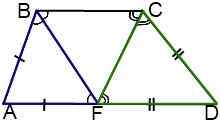
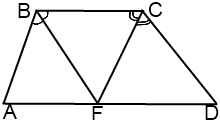 В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.

 

 

 

 Отсюда AD=AF+FD=AB+CD.

 

 

 

Вывод:

Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.

У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.