« »

Рубрика: Комбинации геометрических тел

Призма вписана в цилиндр

Призма вписана в цилиндр, если ее основания — многоугольники, вписанные в основания цилиндра, а боковые ребра являются образующими призмы.

призма, вписанная в цилиндр

прямоугольный параллелепипед в цилиндре

 

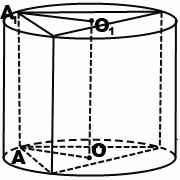
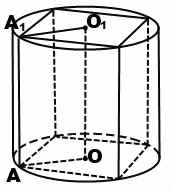
Высоты вписанной призмы и цилиндра равны.

В школьном курсе изучается только прямой круговой цилиндр, соответственно, вписанная в цилиндр призма также должна быть прямой.

Призма может быть вписана в цилиндр, если около ее основания можно описать окружность. Отсюда следует, в цилиндр можно вписать любую правильную призму, прямую треугольную призму, прямоугольный параллелепипед.

В ходе решения задач на призму, вписанную в цилиндр, можно рассмотреть часть осевого сечения комбинации тел — прямоугольник, стороны которого равны радиусу описанной около основания призмы окружности ( радиусу цилиндра) и высоте призмы (и цилиндра). Например, в прямоугольнике AA1O1O OO1=H — высота призмы и цилиндра, AO=R — радиус описанной окружности.

Найдем отношение объема призмы к объему описанного около нее цилиндра:

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{S_{ocn}} \cdot H}}{{\pi {R^2}H}} = \frac{{{S_{ocn}}}}{{\pi {R^2}}}.\]

В частности, отношение объема правильной треугольной призмы к объему описанного цилиндра

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{S_{ocn}}}}{{\pi {R^2}}} = \frac{{\frac{{{a^2}\sqrt 3 }}{4}}}{{\pi {{(\frac{a}{{\sqrt 3 }})}^2}}} = \frac{{{a^2}\sqrt 3 }}{{4\pi \cdot {{\frac{a}{3}}^2}}} = \frac{{3\sqrt 3 }}{{4\pi }}.\]

Отношение объема правильной четырехугольной призмы (то есть прямоугольного параллелепипеда, в основании которого лежит квадрат) к объему описанного около нее цилиндра равно

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{S_{ocn}}}}{{\pi {R^2}}} = \frac{{{a^2}}}{{\pi {{(\frac{a}{{\sqrt 2 }})}^2}}} = \frac{{{a^2}}}{{\frac{{\pi {a^2}}}{2}}} = \frac{2}{\pi },\]

Отношение объема правильной шестиугольной призмы к объему описанного около нее цилиндра

    \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{S_{ocn}}}}{{\pi {R^2}}} = \frac{{\frac{{3{a^2}\sqrt 3 }}{2}}}{{\pi {a^2}}} = \frac{{3\sqrt 3 }}{{2\pi }}.\]

(Как запомнить формулу для вычисления площади правильного шестиугольника, можно посмотреть здесь).

Отношение боковой поверхности вписанной призмы к объему описанного цилиндра:

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}} \cdot H}}{{2\pi RH}} = \frac{{{P_{ocn}}}}{{2\pi R}}.\]

Для правильной треугольной призмы это отношение равно

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi R}} = \frac{{3a}}{{2\pi \cdot \frac{a}{{\sqrt 3 }}}} = \frac{{3\sqrt 3 }}{{2\pi }},\]

для правильной четырехугольной —

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi R}} = \frac{{4a}}{{2\pi \cdot \frac{a}{{\sqrt 2 }}}} = \frac{{2\sqrt 2 }}{\pi },\]

для правильной шестиугольной —

    \[\frac{{{S_1}}}{{{S_2}}} = \frac{{{P_{ocn}}}}{{2\pi R}} = \frac{{6a}}{{2\pi a}} = \frac{3}{\pi }.\]

Ваш отзыв , 15 Мар 2013

Ваш отзыв