sin (2 arcsin x)

Рассмотрим, как найти sin (2 arcsin x). Как и в случае с sin (2 arctg x), для начала воспользуемся формулой синуса двойного угла: sin 2α = 2sinαcosα.

Применяя эту формулу для нашего случая, получаем:

sin (2 arcsin x) = 2 ∙ sin ( arcsin x) ∙ cos ( arcsin x).

Поскольку

$\sin (\arcsin x) = x,npu\left| x \right| \le 1,$

остается найти cos ( arcsin x).

Пример

Найти sin (2 arcsin 3/5).

Решение:

sin (2 arсsin 3/5)

$\sin (2\arcsin \frac{3}{5}) =$

$= 2 \cdot \sin (\arcsin \frac{3}{5}) \cdot \cos (\arcsin \frac{3}{5}) =$

$= 2 \cdot \frac{3}{5} \cdot \cos (\arcsin \frac{3}{5}) = \frac{6}{5}\cos (\arcsin \frac{3}{5}).$

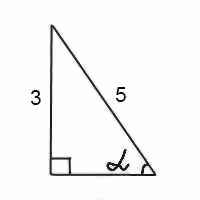
arcsin(3/5) — это угол альфа, синус которого равен 3/5. В прямоугольном треугольнике синус — это отношение противолежащего катета к гипотенузе. А нам нужно найти косинус этого же угла альфа. Косинус — это отношение прилежащего катета к гипотенузе. Прилежащий катет находим по теореме Пифагора:

$\sqrt {{5^2} - {3^2}} = \sqrt {16} = 4.$